The Wiki for Tale 5 is in read-only mode and is available for archival and reference purposes only. Please visit the current Tale 11 Wiki in the meantime.
If you have any issues with this Wiki, please post in #wiki-editing on Discord or contact Brad in-game.
Difference between revisions of "User:McArine/Incense"
| Line 44: | Line 44: | ||
So the formula becomes: | So the formula becomes: | ||
| − | a² + r² = (Dq + r)² | + | a² + r² = (Dq + r)² |
This can be transformed into | This can be transformed into | ||
| − | + | a² + Dq² | |
| − | r = -------- | + | r = -------- |
2*Dq | 2*Dq | ||
Revision as of 17:58, 3 February 2011
My approach to determining incense coordinates
For a long time I tried to find optimum coordinates, by doing exhaustive searches, that would fit the best.
But seeing that none of my results were any good, I considered other approaches.
In T4 the formula for calculating incense qualities was found, and we can see that it hasn't changed in T5.
The current location in simple form:
7*Sx + n*Rx
Xn = ------------
7 + n
7*Yx + n*Yx
Yn = ------------
7 + n
This is the current location between Startpoint and Resinpoint, where n is the amount of resin added.
This gives us a string of locations that are dependent upon the Start and Resin points.
At each of these points we have a quality measure, and an attribute, that indicates to us, how far we are from the closest attribute.
As we don't know the location of the Attribute point, we don't know how far away it is, we just know how much closer to, or further away from the point we get, each time we add a deben of resin.
So that was initially what I used to calculate locations, the difference in quality, between to deben of resin.
Then one day, I drew something like this:
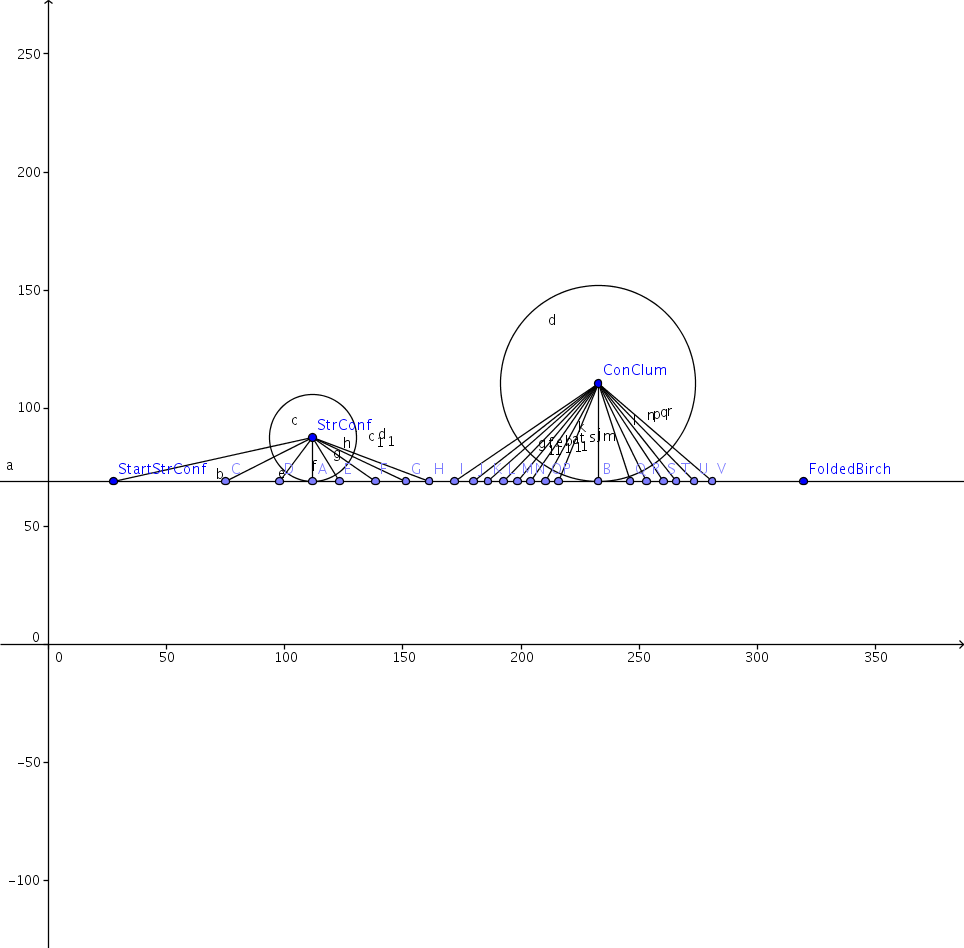
And realised that I had a lot of right angle triangles in this image. I didn't know the exact location where the circle intersected the line, because I didn't know the size of the circle. So what's good about this.
Well, when you test your resin, you get a lot of data, and from this, you can see between which two points the line is closest. You can also get a good estimate of how large the circle is. By looking at the quality from those two points. And this helps us a lot.
Where you previously brute forced through a lot of coordinates, without much accuracy. With this approach you only have to move one coordinate, then the rest can be calculated. Then you just need to estimate the intersection between the circle and the line, and you know got a pythagorean triangle. That you can simply verify the sizes of, by calculating the hypotenuse.
The math is like this:
a² + b² = c²
Where a is the estimated distance between your (Xn, Yn) and the intersection of the circle and the line.
b is the distance from the intersection to the circle center.
And c is the distance between the (Xn, Yn) and the circle center.
Now a is depending on the distance between S and R, and also on the intersection, which is also depending on the distance between S and R. (and we need to try all locations between the two maximum quality points.)
b is the radius of the circle: r.
c is the radius of the circle, plus the difference in quality from (Xn, Yn) to the center(Dq). And we have a good estimate of this.
So the formula becomes:
a² + r² = (Dq + r)²
This can be transformed into
a² + Dq²
r = --------
2*Dq
And for each n location on the line between R and S, that had the same closest attribute. rn can be calculated, and compared to the others, until the best location is found.
Using this formula I can calculate a very good location in less than 1 second, with 0.1 accuracy. This would take hours using my first approach.
Some notes: this works best when using values that differ by more than 20 from start to max. The formula does not figure out if the actual location of A is positive or negative.