User:McArine/Incense

My approach to determining incense coordinates

For a long time I tried to find optimum coordinates, by doing exhaustive searches, that would fit the best.
But seeing that none of my results were any good, I considered other approaches.

In T4 the formula for calculating incense qualities was found, and we can see that it hasn't changed in T5.
The current location in simple form, using only 1 resin:

     7*Sx + n*Rx
Xn = ------------
       7 + n       

     7*Sy + n*Ry
Yn = ------------
       7 + n 

This is the current location between Startpoint and Resinpoint, where n is the amount of resin added.
This gives us a string of locations that are dependent upon the Start and Resin points.
At each of these points we have a quality measure, and an attribute, that indicates to us, how far we are from that closest attribute.

As we don't know the location of the Attribute point, we don't know how far away it is, we just know how much closer to, or further away from the point we get, each time we add a deben of resin.
So that was initially what I used to calculate locations, the difference in quality, between two deben of resin.
And the maths for this gets a bit hairy, I can tell you.

Then one day, I drew something like this:

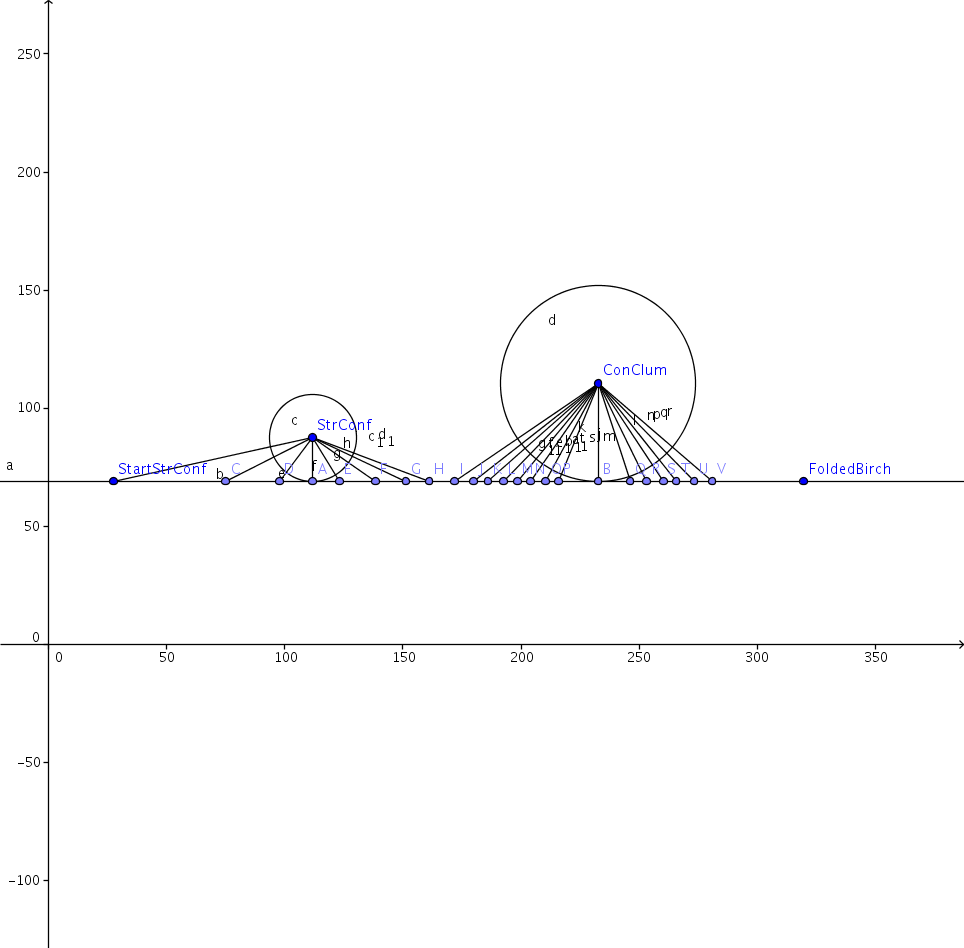
And realised that I had a lot of right angle triangles in this image. I didn't know the exact location where the circle intersected the line, because I didn't know the size of the circle... So what's good about this.

Well, realizing this you can build a simpler program, that can figure out the distance between Start and Resin points. Can calculate where the Attribute point is closest, at what distance it is from the line between Start and Resin points. And another cool thing, you can get how far from the start attribute, the start point is. And these things helps us a lot.
Where you previously brute forced through a lot of coordinates, without much accuracy. This approach can be done with three loops, in a program. But you don't know any boundaries for those loops.
The new approach also takes three loops. But the range these cover is a lot smaller. The first loop varies the distance between Start and Resin point(we assume they're both on the x-axis, and that the Start point is at 0,0). The second loop varies between the two maximum quality values, that's where we have the closest point. The third loop varies the distance from the Attribute to the Start-Resin line, this value will (allways, because Teppy likes the Floor function) be larger than the highest quality value of that Attribute.
I know that using a value equal to or larger than the best quality, doesn't give you the distance from the line to the Attribute point. But with a bit of math we don't need it, we just need to know the difference between that value and the quality value we use on the hypotenuse.
Now, with the closest point, the distance to the Attibute, and the quality of the other points, we can calculate a lot of pythogerean triangles. Compare the resulting values, and see if the location we have found is a good match.

The math is like this:

a² + b² = c²

Where a is the estimated distance between your (Xn, Yn) and the intersection of the circle and the line(the closest point found in loop 2).
b is the distance from the intersection to the circle center(the one to be eliminated).
And c is the distance between the (Xn, Yn)(from above) and the circle center(Attibute point).

Now a is depending on the distance between S and R, and also on the intersection, which is also depending on the distance between S and R. (and we need to try all locations between the two maximum quality points, loop 1 and loop 2)
b is the radius of the circle: r. c is the radius of the circle, plus the difference in quality from (Xn, Yn)(the value from our test) to the center(the value we have from loop 3), lets call it Dq.

So the formula becomes:

a² + r² = (Dq + r)²

This can be transformed into

    a² + Dq²
r = --------
     2*Dq

And for each n location on the line between R and S, that had the same closest attribute. rn can be calculated, and compared to the others, until the best location is found.
So this best value gives us the distance between R and S, the smallest distance to A and the location of that distance on the S-R line. I also promised the distance to the starting point. It can be calculated as the following:

The way that quality is calculated is 1000 - Resin - Herb - Rose. Where Resin, Herb and Rose is the distance from the current location in the three planes to the closest Attribute in that plane. So if we're 55 coords from StrClum in Resin, 42 coords from Honey in Herb and 149 from Invigorating in Rose, the quality is 1000 - 55 - 42 - 149 = 754.
From our program we have, the shortest distance from the S-R line to the Attribute, as a quality value that's higher than the best observed quality. We also have the radius of the circle, which is the actual distance from the Attribute to the R-S line.
So the best possible quality we can achieve is on top of the Attribute, so this is B = r + best value(from loop 2). This would give us a distance of 0 in the quality calculation, so we just need to subtract the starting value from B to get the starting distance.
E.g. if starting value is 644, radius is 55 and best value is 754, we get the start distance as: (754 + 55) - 644 = 165 coords.

Using this formula I can calculate a very good location in less than 1 second, with 0.1 coordinate accuracy. This would take hours using my first approach.

Some notes: this works best when using values that differ by more than 20 from start to max.
The formula does not figure out if the actual location of A is positive or negative.
I don't have a minimum requirement for number of locations for calculating using this approach, but I've had good results using 7 points, I've also been able to get good results from 4 points with large differences.