The Wiki for Tale 5 is in read-only mode and is available for archival and reference purposes only. Please visit the current Tale 11 Wiki in the meantime.
If you have any issues with this Wiki, please post in #wiki-editing on Discord or contact Brad in-game.
User:Sonea
The "Acroloop" system
What it is
The acroloop system is suitable for a medium sized group of people who want to acro, say after a dig or similar event. It has the advantage of no waiting queue where everybody gets to acro with everybody. It works for all sizes but it isn't recommended to extend it while in the middle of a run. It helps to have stations marked at regular acro distances but isn't strictly needed.
How it works
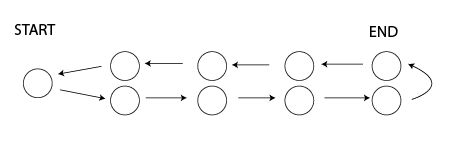
- Everybody pair themselves two and two creating a line
- Assuming an odd number of participants, one person stand alone at beginning of line. (If even number see below.)
- While acroing with your first partner, choose who go FORWARD and who go BACKWARD. Make sure you and your partner move in different directions.
- Each three minutes (proposing when your "hi" message in main chat turn 3 minutes old) everybody rotates. Go towards your designated direction and keep this direction every rotation.
- At end station instead of moving forward you remain stationary one rotation and then move backwards next one. (You acro twice at the end station.) The first round, the two people at end station should determine who shall go back and who shall stay.
- The single person at start gets a coffee break for this round and then always goes forward at rotation.
All the above can be summarized with the diagram below:
When will it end?
After N rounds where N is number of participants you will meet your original partner again at the same location where you started. At this point, everybody will have acroed with everybody else. At least in theory. :)
Even number of participants
If there is an even number of participants, one can use the exact same method with the only addition of a stationary person at the start station.